Определение статистических характеристик волнения и качки судна
Волны, созданные ветром на поверхности моря, лишь на первый взгляд кажутся однородными и правильными (т. е. имеющими одинаковые амплитуды и периоды). Инструментальные наблюдения показывают, что последовательные волны изменяются в широких пределах по высоте, периоду и форме. Поэтому качка судна в море нерегулярна и также изменчива и лишена видимой закономерности, как и колебания поверхности моря. Морское волнение и вызванные им колебания судна (качка, ускорения и т. д.) являются случайными процессами, реализации которых представляют последовательности случайных величин [6, 9]. В отличие от неслучайных (детерминированных) величин для случайной величины нельзя предсказать точно, какое она примет значение в определенных, внешне одинаковых условиях, а можно только указать соответствующий закон распределения вероятностей, который определяет вероятность того, что рассматриваемая случайная величина х не превосходит заданное значение X
![]()
Важнейшими статистическими характеристиками случайной величины являются математическое ожидание (среднее значение) х и дисперсия Dx, которые для непрерывной случайной величины х, имеющей плотность вероятности ƒ(х), вычисляют по формулам

где х2—средний квадрат величины х.
Для практических оценок интенсивности случайных процессов удобно использовать среднее квадратическое отклонение величины х, которое имеет размерность х и называется ее стандартом
![]()
При изучении волнения и мореходности судов кроме функции распределения широко применяется понятие обеспеченности
![]()
которая определяет вероятность неравенства х≥Х и, следовательно, для непрерывной случайной величины представляет собой вероятность превышения заданного значения этой величины.
При произвольном законе распределения вероятностей для ограниченной случайной величины

т. е. среднее значение случайной величины равно площади, ограниченной функцией Р(х). Это свойство функции обеспеченности полезно использовать при статистической обработке экспериментальных данных.
Для стационарных условий испытаний среднее значение и дисперсия процессов качки и волнения не зависят от времени и на основании эргодиче-ской теоремы могут быть определены по одной «типичной» реализации процесса x(t), записанной в интервале времени (0, Т)

Пример такой реализации показан на рис. 101, на котором содержатся все основные особенности действительных записей волнения и качки. Для определения статистических характеристик используют следующие геометрические элементы реализации случайного процесса: ординаты кривой x(t);
амплитуды x0i=x(Ai), рассматриваемые как основные (наибольшие) экстремумы кривой x(t) в промежутке между соседними пересечениями нулевого уровня процесса на восходящем и нисходящем участках;
размахи колебаний (удвоенные амплитуды) Нj=2x0j=x0i — х0(i+1). Они равны расстоянию по вертикали между основными экстремумами (наибольшим максимумом и наименьшим минимумом) кривой x(t), которые расположены внутри двух соседних полупериодов, ограниченных точками перехода процесса x(t) через нулевой уровень в одном направлении. Для волнограмм размах колебаний отождествляется с высотой волны;
полупериоды колебаний 1/2T0i = t (0i + 1) — t (0i), определяемые по интервалам между ближайшими пересечениями нулевого уровня процесса; полупериоды колебаний 1/2Tj = t(Ai+1) — t (Ai), которые определяют по интервалам между смежными основными экстремумами, соответствующими размаху колебаний 2х0j,
периоды колебаний T0j — t(Oi+2)—t(0i), определяемые по интервалам между переходами процесса через нулевой уровень в одном направлении.
Кроме перечисленных основных элементов реализаций случайных процессов иногда рассматривают так называемые вторичные колебания, которые представляют собой относительно мелкие и высокочастотные флюктуации, накладывающиеся на основные колебания. Вторичные колебания связаны с парными экстремумами хmk=х(Эk), расположенными обычно по одну сторону от нулевой линии процесса (рис. 101). Разность hk=|xmk — xm(k+1)| обусловливает величину размаха с учетом вторичных колебаний. При учете вторичных колебаний рассматривают период Tmk = t(Эk+2)—1(Эk), определяемый интервалом между ближайшими максимумами или минимумами, которые могут располагаться в отличие от основных экстремумов по разные стороны нулевой линии записи.
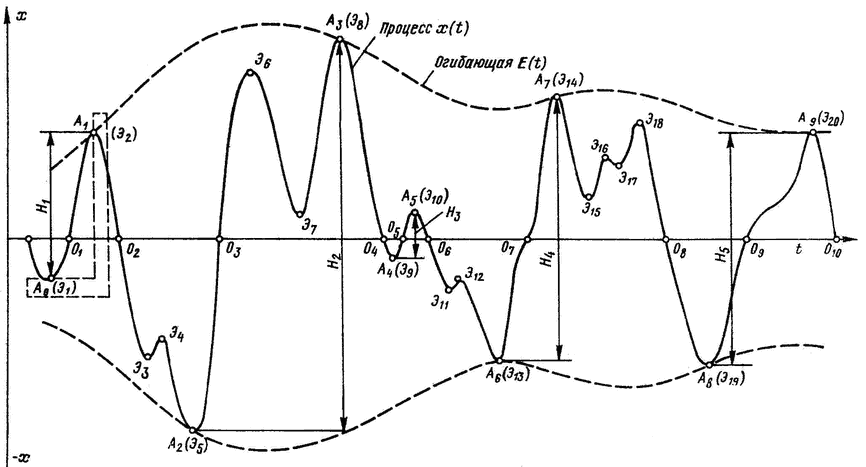 Рис. 101. Типичная реализация случайного процесса. ______________ процесс x(f);— — — огибающая E(t).
Рис. 101. Типичная реализация случайного процесса. ______________ процесс x(f);— — — огибающая E(t).
Ценным свойством рассмотренных элементов реализаций случайных процессов является то, что они поддаются однозначному формальному определению и вследствие этого могут измеряться аппаратурными средствами без использования непрерывной графической записи процесса. Определение законов распределения этих элементов, параметры которых могут быть, как правило, выражены через моментные характеристики энергетических спектров изучаемых процессов, позволяет установить связь между статистическими и спектральными характеристиками, что особенно ценно для практического приложения. В частности, это относится к указанному определению амплитуды, величина которой характеризует максимальное за полупериод отклонение случайного процесса от нулевого уровня и может рассматриваться как ордината огибающей процесса (пунктирная линия на рис. 101). Именно такие отклонения представляют обычно наибольший практический интерес, и в то же время для амплитуды может быть установлена простая связь с параметрами энергетического спектра процесса. Использование наряду с термином «амплитуда» понятия «размах колебаний», которое для случайных колебаний не поддается столь же отчетливой физической интерпретации, обусловлено лишь большей простотой измерения размахов качки по сравнению с ее амплитудами, для определения которых на графике процесса необходимо проводить нулевую линию, а также тем, что оценку интенсивности волнения в баллах, согласно принятой в СССР шкале, производят по высоте (размаху) волн.
Страницы: 1 2 3 4 5